How can we discover the ultimate physical/mathematical laws which govern its evolution in time – or govern its state across space-time?
2006 03 14
By Paul Werbos | werbos.com

Article from Light Eye
Because this a very complex subject, because you all start out
in different places, and because I see an unconventional way
to put togther the very complicated mathematical concepts of mainstream physics,
let me start out with the general picture as I see it.
The General Picture
At the United Nations University
on consciousness in 1999, the organizer, a Japanese physicist, asked us all to
start out with a very brief haiku-like summary of what is different
about our viewpoint. I said:
“Reality is strange but real.
We need more color in our lives
and less in our quarks.”
Today I would add:
“Quantum field theory (QFT) says that objective reality does not exist.
But objective reality says that QFT does not exist (mathematically).
Only if both ghosts reconcile and rise above the flat earth can either one become solid.”
This path has taken me to visit
and study very closely much of the work of the great experimentalist, Prof. Yanhua Shih. Shih’s
experiments with quantum optics, ”Bell’s Theorem” experiments, quantum teleportation, quantum lithography and so
on are perhaps the most complete and accurate in the world. I have often
wondered: how can people talk about quantum measurement for years and years,
and profess to be experts, without taking a very long and hard look at the best
empirical data – in its full depth and richness – about how quantum measurement
actually works in the experiments which tell us the most about it?
As I look ahead… I see a possible
path which starts out in the lowlands of much more rigorous mathematical
methods than those now used in high-energy physics, but leads up ahead to
future peaks – obscured somewhat by clouds and uncertainties – of serious
possibilities for enormous technological breakthroughs (and hazards) after we
develop our fundamental understanding
further. It also allows for the possibility that the greater universe – full of
force fields we have yet to fully understand – may be far stranger, in
qualitative terms, than everyday common sense seems to suggest. Just how
strange could it be? Just to begin… go to What is Life?…
or consider the backwards
time interpretation of quantum mechanics which
I first published in 1973, and have refined a great deal since then (and even
since 2000).
Circa 1900, the conventional
wisdom in physics said: “We already know it all, with only a few very small
holes to fill in. These holes in our understanding are so small that they could
not possibly have technological implications…” We have less reason to
believe that today than we did then, and look what happened in the twentieth
century! If we can avoid the historic tendency of aging civilizations to
become jaded and slowly repress creativity and diversity in myriad ways, the
objective opportunities look very exciting.
Today’s high-energy physics has
tended to become very myopic in its focus on large accelerators and collisions
between individual particles. Certainly these accelerators are an important
tool in reasearch, but we should never forget the larger question: what are we
missing by not paying more attention to large scale many-body effects
for anything but the effects of electricity and magnetism? Is it possible that
the elevated realms of grand unified field theory have something to learn from
the humble literature of people who build lasers and chips? Is it even possible
that new technologies could emerge from that way of thinking?
Time, QFT and Objective Reality
First, some basic facts of life for the nonphysicist.
Today’s best empirical understanding of how the universe
works comes from two very different pieces: (1) the “standard model of physics”
(EWT+QCD), which is a specific model within the large class of models called
“quantum field theory” (QFT); and (2) Einstein’s general relativity (GR), which
is an example of what people now call “classical field theory.” GR predicts
gravity, while the standard model predicts almost everything else now known,
with two main exceptions: (1) there are some strange phenomena called
“superweak interactions,” known for decades, and recently studied closely by
CERN’s “Babar” project, but still not understood; and (2) the predictions of
QCD are hard to calculate for most of empirical nuclear physics, forcing the
use of “phenomenological models” for most empirical work.
There are several truly beautiful quantum theories – so
beautiful that many theorists believe “they have to be true” – about how
to reconcile the standard model with GR. The most popular are superstring
theory (and its n-brane variations) and quantum loop gravity ala Hawkings. They
are as elegant, as popular, as authoritative and as beautifully argued as
Aquinas’s “proofs” of the existence of God. But there is no empirical data at
all yet to support these theories (though people have made efforts to try to
find such data, and are still looking).
Even before the first successful QFT was developed,
Einstein, Schrodinger and DeBroglie argued that quantum mechanics had taken a
wrong path. Einstein argued that the intricate complexities of quantum mechanics
could perhaps be explained as an emergent statistical outcome of a more
fundamental “classical field theory” operating over space-time. In such a
theory, the entire state of reality can be specified in principle by specifying
the state of a finite number of “fields” (force fields) over space-time; each
field is basically just a nice, continuous differentiable function, defined
over Minkoswki space. The “law of evolution” of these fields is a set of local
relationships, called “partial differential equations” (PDE) or “wave
equations.” My first heresy is that I believe that Einstein was right after all
– and, furthermore, that I can see where to find a set of PDE which can do the
job. The key papers which explain this are, in chronological order:
The Backwards-Time Interpretation of Quantum Mechanics - Revisited With Experiment
Realistic Derivation of Heisenberg Dynamics
Equivalence of Classical Statistics and Quantum Dynamics of Well-Posed Bosonic Field Theories
Proof of Partial Equivalence of Classical and Quantum Dynamics in Bosonic Systems
A Conjecture About Fermi-Bose Equivalence
Is all of this just a matter of philosophy? Does it make any
difference to empirical reality? Consider, for example, the following question:
what will happen if we find really new experimental setups, different
from what has happened by accident already in the atmosphere, which can produce
small black holes? (Several major labs are spending money on major efforts to
do just that.) According to Hawking, and according to superstring theories
which rely on Hawking-style approximations, the black holes will simply just
evaporate away very quickly. But a unification based on Einstein’s approach
would probably support the original prediction from the Einstein school – the
prediction that a small black hole would gradually grow over a few thousand
years, hidden away inside the earth, and then suddenly gobble up the earth in an
unforeseen catastrophe rather similar to the comic book story about the planet
Krypton. Does it really matter whether the entire planet earth might be gobbled
up? To some of us it would. This is only a hypothetical example, but it would
be nice to know what the true story is.
More seriously – years ago I started to prove and publish
theorems showing that the statistics which emerge from “classical” PDE are more
or less equivalent to those implied by the dynamic laws of quantum mechanics. (For
a more precise statement, click on the papers above.) When I did so, there were
two groups of people who reacted very differently to this. One group said that
this was utterly impossible and utterly crazy. (No, they didn’t suggest any
flaw in the logic; it was essentially a group loyalty kind of thing.) The other
big and established group in physics said “Oh, we already knew that.” The second
group were the people who knew how to build real technologies with lasers, with
quantum optics. Classical-quantum equivalence turns out to be absolutely
essential as a practical mathematical tool in building a host of modern devices
like lasers – devices which exploit many-body effects. What I had discovered
was really a kind of easy generalization and (more important) a new way of using
that kind of mathematics – but the same principles were in regular use every
day, an essential tool in the exploitation of many-body effects to generate
large physical effects from things which might seem very small. The easiest
standard introduction to classical-qauntum equivalence can be found in chapter
4 of Quantum Optics, by Walls and Milburn, but a more rigorous version
appears in Chapter 3 of Howard J. Carmichael’s book on statistical physics; the
material is also discussed in chapter 11 of Optical Coherence and Quantum
Optics by Mandel and Wolf, after a long discussion of practical
semiclassical methods. If people can now produce X-ray lasers and atom lasers…
who knows what else we can do? Could we do things that do not happen by chance in
nature with any significant probability… like breaking down the “mass gap” that
prevents us from converting protons and neutrons directly into energy? Or like
refining nuclear physics in the way we refined quantum optics years ago, based
on empirical data and an open mind? But I do hope that anyone who explores this
will maintain a link to the paragraph above, and be careful. Becoming famous
won’t help you much if we all end up dead.
Many physics courses today begin with a long list of reasons
why Einstein could not possibly have been right. In many cases, however, the
list is intended to motivate introductory study of quantum mechanics, rather
than to explain what is really going on. For example, many would say “classical
physics is the limiting case where Planck’s constant (h) goes to zero; however,
since h is not zero, we know CFT must be wrong.” But in fact, when h goes to
zero, we end up with a physics in which the entire universe is made up of exact
point particles. That isn’t at all the same as the continuous universe Einstein
was proposing! Likewise, many rely heavily on intuitive understanding of
Heisenberg’s uncertainty principle, which isn’t really part of the underlying
mathematics of QFT; an experiment which brings that out is posted at:
Experimental realization of Popper's Experiment: Violation of the Uncertainty Principle?
The most serious researchers in quantum foundations would
point towards the “Bell’s
Theorem” experiments (and variations thereof) as the main reason to rule out
Einstein’s concept today. Most people have learned about these experiments from
the authoritative well-known book: J.S.Bell, The Speakable and Unspeakable in Quantum Mechanics, Cambridge U.
Press, 1987. Bell
describes how a certain key theorem was actually proved and published by
Clauser, Holt, Shimony and Horne. He then states: if we accept that experiment
described in this theorem has been done, that it agrees with quantum mechanics
– and, more important – that it is “close enough” to the predictions of quantum
mechanics, that we must give up either the concept of objective reality,
or give up the concept of “locality” hardwired into CFT. The “Copenhagen version” of quantum mechanics
gives up objective reality, while the Bohmian version (and its cousins) give up
locality, mainly by assuming that the cosmos is infinite-dimensional at the end
of the day.
But Bell’s book leaves out a third possibility. I was very fortunate, during graduate
school, to be able to speak frequently with Richard Holt – a fellow student –
as he set up one of the two first experiments to implement this theorem. (But
on the negative side, I allowed myself to overreact in horror with certain
aspects of all this, and I still regret a paper I published in Nuovo Cimento in
1977 based on that overreaction.) He
showed me a more precise, more original mathematical paper showing that the
experiment would rule out at least one of: (1) “hidden variables” (reality);
(2) locality; and (3) time-forwards causality covering all inputs and
outputs of the experiment. Thus it is only natural that I published the
first paper, back in 1973, which stressed this third loophole: the possibility
of a local realistic model – even a CFT model – where we get rid of the ad hoc
arbitrary traditional assumption that “causality” can only flow forwards in
time.
Some physicists now argue:
“My brain cannot imagine a universe in which causality does not always flow
forwards in time. That is hardwired into all of our brains.” But that is
exactly the same as what the Cardinals were saying back at the time of
Copernicus. People said “the direction down is hardwired into our very bodies
and minds. Therefore, it must be the same direction in all places in the entire
universe. Therefore the world must be flat. In any case, our minds are designed
to assume this, and cannot possibly learn to live with any other point of
view.” Wrong, wrong, wrong. There is no more reason for the arrow of time to be
a universal invariant at all levels of nature than there is for the direction
“down” to be. And the human brain is perfectly capable of learning to make
predictions based on a more powerful model. (Still, I highly recommend Huw
Price’s work on “overcoming the old double standard about time,” cited in the
links above – though Price
himself recommends a more recent URL.) The true, underlying story here is
as follows: many, many humans would rather insist that the larger universe of
objective reality, does not exist at all, rather than admit that it does not
slavishly and universally follow an anthropocentric coordinate system (for
“down” or for “future”). These points are described in more than enough detail,
for now, in the links above.
During 2002, I had extensive discussions
with Yanhua Shih and with Jon Dowling, and later with Huw Price, about the
concrete explanation of Bell’s
Theorem experiments and about possible new experiments. Crudely, I would
describe the true picture in the Bell’s
Theorem experiments to be a statistical mix of the two pictures
suggested by the work of Klyshko in backwards-time empirical optics, the left
channel picture and the right picture, which can be represented as a Markhov
Random Field over space-time. Klyshko’s work has been the key tool which
enabled Shih’s group to achieve new types of quantum entanglement, essential to
his many successful experiments. There are many important thoughts which merit
following up, but in January
of 2003, I concluded that the first priority, for me, with my limited time,
was to address more fundamental issues regarding quantum dynamics, which lead
to the thoughts below.
The Most Urgent Next Task in Basic (Mathematical) Research
For the time being, I see the most important work needed in basic physics to be basic mathematical work. A very quick summary:
1. When high-energy physics demands that a theory of the universe be
renormalizable, it is demanding, in effect, that a Taylor series about zero must converge. Not
only classical physics, but the quantum theory of solitons, shows that this is not a reasonable requirement. For
example, Rajaraman’s classic book Solitons and Instantons shows how “WKB” – a Taylor series about a
nonzero state – is essential for many models.
2. The price of this unreasonable demand is that large coupling constants are ruled out, and
hence all those bosonic field theories which generate solitons which are
capable of being mathematically meaningful without renormalization! In
order to avoid the weird ad hoc assumption that God somehow intervenes to
gobble up the infinite energy of self-repulsion that comes with point particle
models, and in order to have a truly well-posed mathematical model, we need a
new approach to axiomatic theory and a nonperturbative foundation. (Others like
Arai have said this much, but more people need to listen.)
3. Many physicists would prefer to find an axiomatic
formulation of QFT which starts from the nice clean elegant picture of
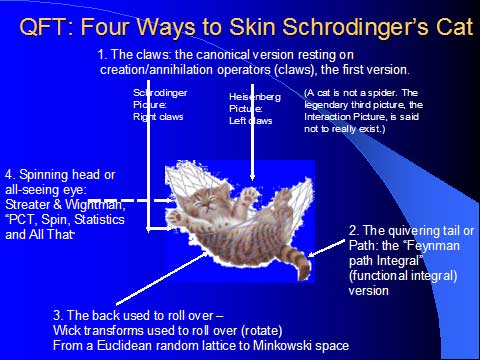
Streater and Wightman (see the image on the right). But this has not really
worked, for a variety of reasons. Perhaps it would be more realistic to start
from the original, canonical version of QFT (as in Mandl and Shaw), and show
how that can constitute a well-posed nontrivial dynamical system. Some ideas on
those lines are given in A
Conjecture About Fermi-Bose Equivalence. To get back to elegance, we
can then exploit the quantum-classical equivalence relations, which turn out to
be mirror images and generalizations of mappings previously discussed by
Glauber and Wigner, widely used in quantum optics widely used in quantum
optics.
4. Even at the classical level, the most well-studied wave equations tend to generate singularities (blow-up and
ill-posedness) or else be “trivial,” in the sense that energy dissipates away
into infinitely weak radiation. The only real exceptions are models which
generate something like solitons. More precisely, models which generate true or
metastable “chaoitons” as discussed in New
Approaches to Soliton Quantization and Existence for Particle Physics. Thus for a nontrivial
well-defined QFT, this classically-motivated approach is the most promising
available.
5. A careful study of Walter Strauss’s monograph suggests that a proper starting point is to
prove similar inequalities – like Holder and Sobolev inequalities – for quantum
mechanical expressions, using normal products, starting from an
initial state defined by some smooth initial density matrix with compact
support.
6. In New Approaches to Soliton
Quantization and Existence for Particle Physics, Ludmilla and I had
some difficulty in finding a counterexample to the conjecture by Markhankov,
Rybakov and Sanyuk that stable “solitons” can only exist in classical field
theories which are “topologically nontrivial.” I now suspect that such an
example could be constructed simply by considering a bound state of a pair of
‘tHooft or ‘tHooft/Hasenfratz patterns, which are acceptable in CFT only when
bound together (because of boundary conditions). Particles constructed in this
matter should be able to model fermions, in a very general way, and thus the
entire standard model.
Article from: http://www.werbos.com/reality.htm
Related: Holographic Reality & Spritual Science
